Note
Click here to download the full example code or to run this example in your browser via Binder
Classification of age groups using functional connectivity#
This example compares different kinds of functional connectivity between regions of interest : correlation, partial correlation, and tangent space embedding.
The resulting connectivity coefficients can be used to discriminate children from adults. In general, the tangent space embedding outperforms the standard correlations: see Dadi et al 2019 for a careful study.
Note
If you are using Nilearn with a version older than 0.9.0,
then you should either upgrade your version or import maskers
from the input_data module instead of the maskers module.
That is, you should manually replace in the following example all occurrences of:
from nilearn.maskers import NiftiMasker
with:
from nilearn.input_data import NiftiMasker
Load brain development fMRI dataset and MSDL atlas#
We study only 30 subjects from the dataset, to save computation time.
from nilearn import datasets
development_dataset = datasets.fetch_development_fmri(n_subjects=30)
We use probabilistic regions of interest (ROIs) from the MSDL atlas.
msdl_data = datasets.fetch_atlas_msdl()
msdl_coords = msdl_data.region_coords
n_regions = len(msdl_coords)
print('MSDL has {0} ROIs, part of the following networks :\n{1}.'.format(
n_regions, msdl_data.networks))
MSDL has 39 ROIs, part of the following networks :
['Aud', 'Aud', 'Striate', 'DMN', 'DMN', 'DMN', 'DMN', 'Occ post', 'Motor', 'R V Att', 'R V Att', 'R V Att', 'R V Att', 'Basal', 'L V Att', 'L V Att', 'L V Att', 'D Att', 'D Att', 'Vis Sec', 'Vis Sec', 'Vis Sec', 'Salience', 'Salience', 'Salience', 'Temporal', 'Temporal', 'Language', 'Language', 'Language', 'Language', 'Language', 'Cereb', 'Dors PCC', 'Cing-Ins', 'Cing-Ins', 'Cing-Ins', 'Ant IPS', 'Ant IPS'].
Region signals extraction#
To extract regions time series, we instantiate a
nilearn.maskers.NiftiMapsMasker object and pass the atlas the
file name to it, as well as filtering band-width and detrending option.
from nilearn.maskers import NiftiMapsMasker
masker = NiftiMapsMasker(
msdl_data.maps, resampling_target="data", t_r=2, detrend=True,
low_pass=.1, high_pass=.01, memory='nilearn_cache', memory_level=1).fit()
Then we compute region signals and extract useful phenotypic information.
children = []
pooled_subjects = []
groups = [] # child or adult
for func_file, confound_file, phenotypic in zip(
development_dataset.func,
development_dataset.confounds,
development_dataset.phenotypic):
time_series = masker.transform(func_file, confounds=confound_file)
pooled_subjects.append(time_series)
if phenotypic['Child_Adult'] == 'child':
children.append(time_series)
groups.append(phenotypic['Child_Adult'])
print('Data has {0} children.'.format(len(children)))
Data has 24 children.
ROI-to-ROI correlations of children#
The simpler and most commonly used kind of connectivity is correlation. It
models the full (marginal) connectivity between pairwise ROIs. We can
estimate it using nilearn.connectome.ConnectivityMeasure.
from nilearn.connectome import ConnectivityMeasure
correlation_measure = ConnectivityMeasure(kind='correlation')
From the list of ROIs time-series for children, the correlation_measure computes individual correlation matrices.
correlation_matrices = correlation_measure.fit_transform(children)
# All individual coefficients are stacked in a unique 2D matrix.
print('Correlations of children are stacked in an array of shape {0}'
.format(correlation_matrices.shape))
Correlations of children are stacked in an array of shape (24, 39, 39)
as well as the average correlation across all fitted subjects.
mean_correlation_matrix = correlation_measure.mean_
print('Mean correlation has shape {0}.'.format(mean_correlation_matrix.shape))
Mean correlation has shape (39, 39).
We display the connectome matrices of the first 3 children
from nilearn import plotting
from matplotlib import pyplot as plt
_, axes = plt.subplots(1, 3, figsize=(15, 5))
for i, (matrix, ax) in enumerate(zip(correlation_matrices, axes)):
plotting.plot_matrix(matrix, tri='lower', colorbar=False, axes=ax,
title='correlation, child {}'.format(i))
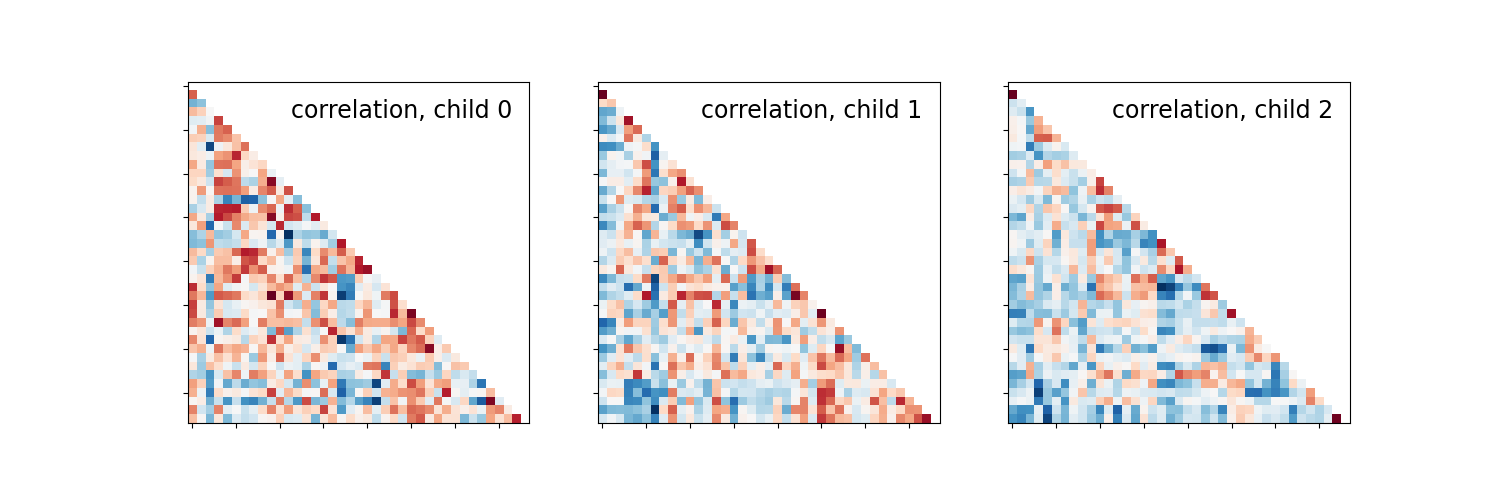
The blocks structure that reflect functional networks are visible.
Now we display as a connectome the mean correlation matrix over all children.
plotting.plot_connectome(mean_correlation_matrix, msdl_coords,
title='mean correlation over all children')
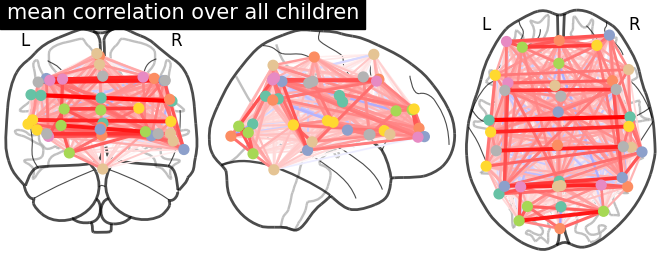
<nilearn.plotting.displays._projectors.OrthoProjector object at 0x7ff8ed1a3040>
Studying partial correlations#
We can also study direct connections, revealed by partial correlation coefficients. We just change the ConnectivityMeasure kind
partial_correlation_measure = ConnectivityMeasure(kind='partial correlation')
partial_correlation_matrices = partial_correlation_measure.fit_transform(
children)
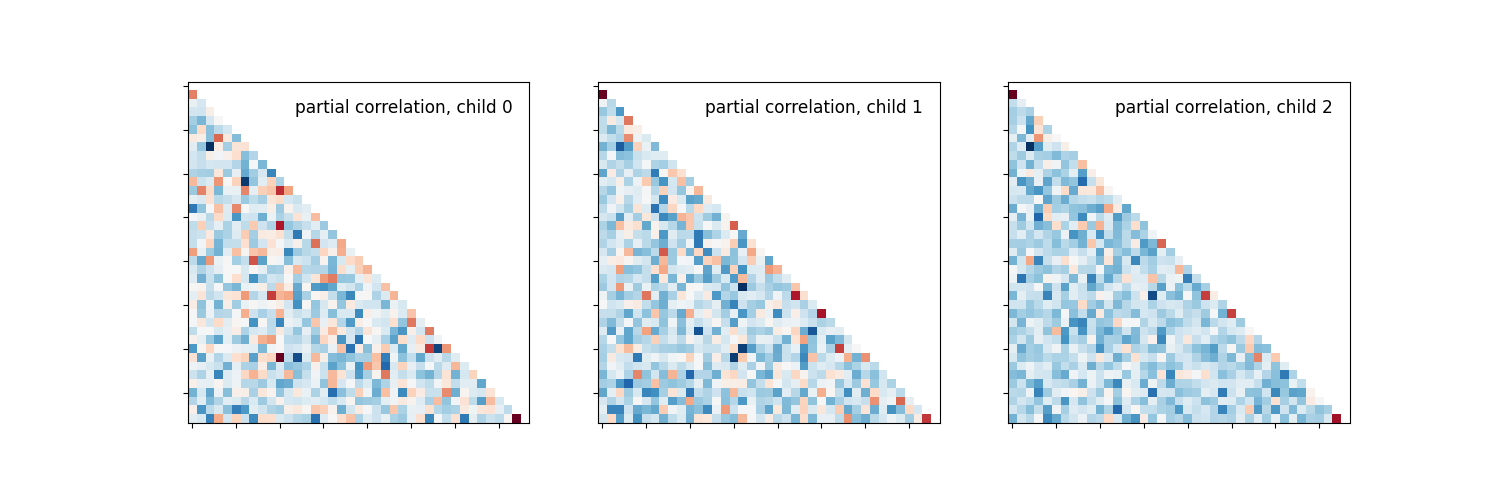
Most of direct connections are weaker than full connections.
_, axes = plt.subplots(1, 3, figsize=(15, 5))
for i, (matrix, ax) in enumerate(zip(partial_correlation_matrices, axes)):
plotting.plot_matrix(matrix, tri='lower', colorbar=False, axes=ax,
title='partial correlation, child {}'.format(i))
plotting.plot_connectome(
partial_correlation_measure.mean_, msdl_coords,
title='mean partial correlation over all children')
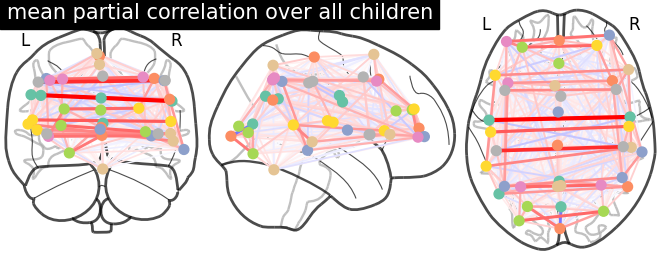
<nilearn.plotting.displays._projectors.OrthoProjector object at 0x7ff8c5f5f2e0>
Extract subjects variabilities around a group connectivity#
We can use both correlations and partial correlations to capture reproducible connectivity patterns at the group-level. This is done by the tangent space embedding.
tangent_measure = ConnectivityMeasure(kind='tangent')
We fit our children group and get the group connectivity matrix stored as in tangent_measure.mean_, and individual deviation matrices of each subject from it.
tangent_matrices model individual connectivities as perturbations of the group connectivity matrix tangent_measure.mean_. Keep in mind that these subjects-to-group variability matrices do not directly reflect individual brain connections. For instance negative coefficients can not be interpreted as anticorrelated regions.
_, axes = plt.subplots(1, 3, figsize=(15, 5))
for i, (matrix, ax) in enumerate(zip(tangent_matrices, axes)):
plotting.plot_matrix(matrix, tri='lower', colorbar=False, axes=ax,
title='tangent offset, child {}'.format(i))
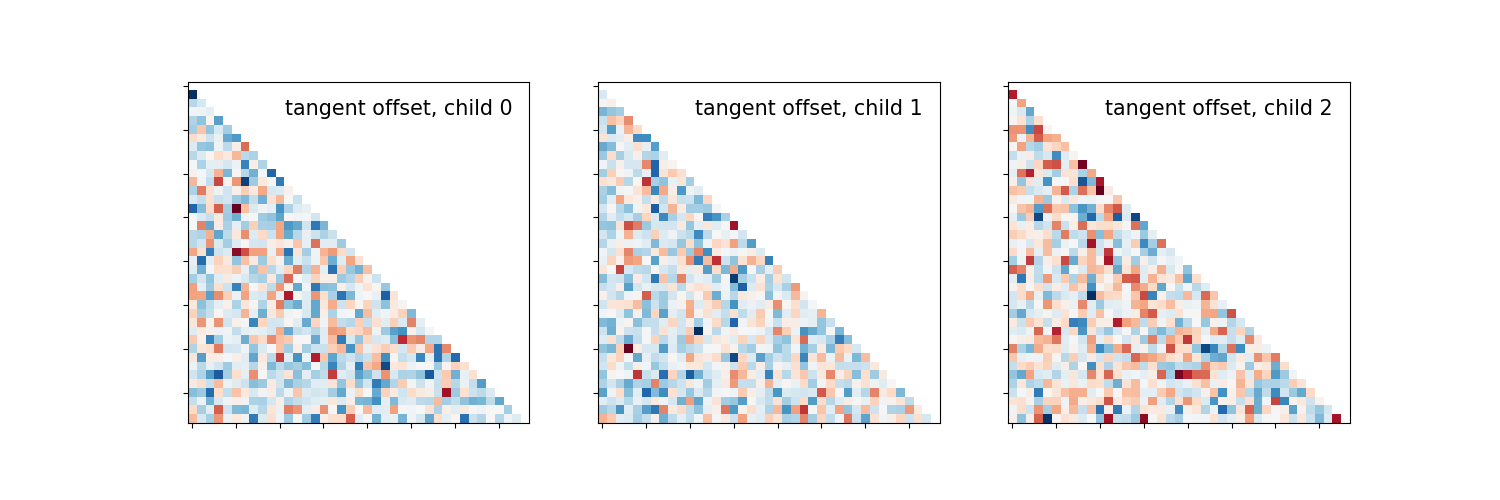
The average tangent matrix cannot be interpreted, as individual matrices represent deviations from the mean, which is set to 0.
What kind of connectivity is most powerful for classification?#
We will use connectivity matrices as features to distinguish children from adults. We use cross-validation and measure classification accuracy to compare the different kinds of connectivity matrices. We use random splits of the subjects into training/testing sets. StratifiedShuffleSplit allows preserving the proportion of children in the test set.
from sklearn.svm import LinearSVC
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.metrics import accuracy_score
import numpy as np
kinds = ['correlation', 'partial correlation', 'tangent']
_, classes = np.unique(groups, return_inverse=True)
cv = StratifiedShuffleSplit(n_splits=15, random_state=0, test_size=5)
pooled_subjects = np.asarray(pooled_subjects)
scores = {}
for kind in kinds:
scores[kind] = []
for train, test in cv.split(pooled_subjects, classes):
# *ConnectivityMeasure* can output the estimated subjects coefficients
# as a 1D arrays through the parameter *vectorize*.
connectivity = ConnectivityMeasure(kind=kind, vectorize=True)
# build vectorized connectomes for subjects in the train set
connectomes = connectivity.fit_transform(pooled_subjects[train])
# fit the classifier
classifier = LinearSVC().fit(connectomes, classes[train])
# make predictions for the left-out test subjects
predictions = classifier.predict(
connectivity.transform(pooled_subjects[test]))
# store the accuracy for this cross-validation fold
scores[kind].append(accuracy_score(classes[test], predictions))
display the results
mean_scores = [np.mean(scores[kind]) for kind in kinds]
scores_std = [np.std(scores[kind]) for kind in kinds]
plt.figure(figsize=(6, 4))
positions = np.arange(len(kinds)) * .1 + .1
plt.barh(positions, mean_scores, align='center', height=.05, xerr=scores_std)
yticks = [k.replace(' ', '\n') for k in kinds]
plt.yticks(positions, yticks)
plt.gca().grid(True)
plt.gca().set_axisbelow(True)
plt.gca().axvline(.8, color='red', linestyle='--')
plt.xlabel('Classification accuracy\n(red line = chance level)')
plt.tight_layout()
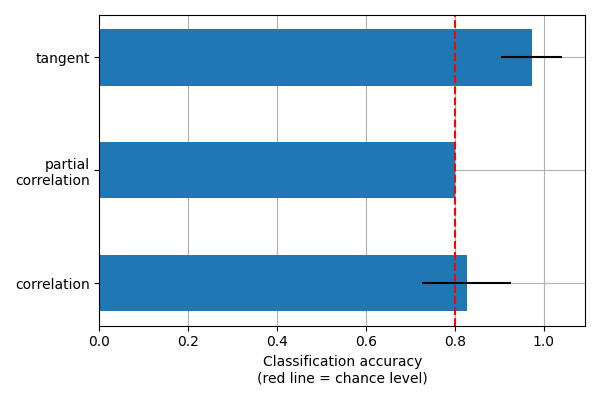
This is a small example to showcase nilearn features. In practice such comparisons need to be performed on much larger cohorts and several datasets. Dadi et al 2019 Showed that across many cohorts and clinical questions, the tangent kind should be preferred.
Total running time of the script: ( 1 minutes 8.796 seconds)
Estimated memory usage: 1042 MB