Note
This page is a reference documentation. It only explains the class signature, and not how to use it. Please refer to the user guide for the big picture.
nilearn.connectome.ConnectivityMeasure#
- class nilearn.connectome.ConnectivityMeasure(cov_estimator=LedoitWolf(store_precision=False), kind='covariance', vectorize=False, discard_diagonal=False)[source]#
A class that computes different kinds of functional connectivity matrices.
New in version 0.2.
- Parameters
- cov_estimatorestimator object, optional.
The covariance estimator. By default the LedoitWolf estimator is used. This implies that correlations are slightly shrunk towards zero compared to a maximum-likelihood estimate
- kind{“covariance”, “correlation”, “partial correlation”, “tangent”, “precision”}, optional
The matrix kind. For the use of “tangent” see 1. Default=’covariance’.
- vectorizebool, optional
If True, connectivity matrices are reshaped into 1D arrays and only their flattened lower triangular parts are returned. Default=False.
- discard_diagonalbool, optional
If True, vectorized connectivity coefficients do not include the matrices diagonal elements. Used only when vectorize is set to True. Default=False.
References
- 1
Gael Varoquaux, Flore Baronnet, Andreas Kleinschmidt, Pierre Fillard, and Bertrand Thirion. Detection of brain functional-connectivity difference in post-stroke patients using group-level covariance modeling. In Tianzi Jiang, Nassir Navab, Josien P. W. Pluim, and Max A. Viergever, editors, Medical image computing and computer-assisted intervention - MICCAI 2010, Lecture notes in computer science, 200–208. Berlin, Heidelberg, 2010. Springer. doi:10/cn2h9c.
- Attributes
- `cov_estimator_`estimator object
A new covariance estimator with the same parameters as cov_estimator.
- `mean_`numpy.ndarray
The mean connectivity matrix across subjects. For ‘tangent’ kind, it is the geometric mean of covariances (a group covariance matrix that captures information from both correlation and partial correlation matrices). For other values for “kind”, it is the mean of the corresponding matrices
- `whitening_`numpy.ndarray
The inverted square-rooted geometric mean of the covariance matrices.
- __init__(cov_estimator=LedoitWolf(store_precision=False), kind='covariance', vectorize=False, discard_diagonal=False)[source]#
- fit(X, y=None)[source]#
Fit the covariance estimator to the given time series for each subject.
- Parameters
- Xlist of numpy.ndarray, shape for each (n_samples, n_features)
The input subjects time series. The number of samples may differ from one subject to another.
- Returns
- selfConnectivityMatrix instance
The object itself. Useful for chaining operations.
- fit_transform(X, y=None, confounds=None)[source]#
Fit the covariance estimator to the given time series for each subject. Then apply transform to covariance matrices for the chosen kind.
- Parameters
- Xlist of n_subjects numpy.ndarray with shapes (n_samples, n_features)
The input subjects time series. The number of samples may differ from one subject to another.
- confoundsnp.ndarray with shape (n_samples) or (n_samples, n_confounds), or pandas DataFrame, optional
Confounds to be cleaned on the vectorized matrices. Only takes into effect when vetorize=True. This parameter is passed to signal.clean. Please see the related documentation for details.
- Returns
- outputnumpy.ndarray, shape (n_subjects, n_features, n_features) or (n_subjects, n_features * (n_features + 1) / 2) if vectorize is set to True.
The transformed individual connectivities, as matrices or vectors. Vectors are cleaned when vectorize=True and confounds are provided.
- transform(X, confounds=None)[source]#
Apply transform to covariances matrices to get the connectivity matrices for the chosen kind.
- Parameters
- Xlist of n_subjects numpy.ndarray with shapes (n_samples, n_features)
The input subjects time series. The number of samples may differ from one subject to another.
- confoundsnumpy.ndarray with shape (n_samples) or (n_samples, n_confounds), optional
Confounds to be cleaned on the vectorized matrices. Only takes into effect when vetorize=True. This parameter is passed to signal.clean. Please see the related documentation for details.
- Returns
- outputnumpy.ndarray, shape (n_subjects, n_features, n_features) or (n_subjects, n_features * (n_features + 1) / 2) if vectorize is set to True.
The transformed individual connectivities, as matrices or vectors. Vectors are cleaned when vectorize=True and confounds are provided.
- inverse_transform(connectivities, diagonal=None)[source]#
Returns connectivity matrices from connectivities, vectorized or not.
If kind is ‘tangent’, the covariance matrices are reconstructed.
- Parameters
- connectivitieslist of n_subjects numpy.ndarray with shapes (n_features, n_features) or (n_features * (n_features + 1) / 2,)
or ((n_features - 1) * n_features / 2,) Connectivities of each subject, vectorized or not.
- diagonalnumpy.ndarray, shape (n_subjects, n_features), optional
The diagonals of the connectivity matrices.
- Returns
- outputnumpy.ndarray, shape (n_subjects, n_features, n_features)
The corresponding connectivity matrices. If kind is ‘correlation’/ ‘partial correlation’, the correlation/partial correlation matrices are returned. If kind is ‘tangent’, the covariance matrices are reconstructed.
- get_params(deep=True)#
Get parameters for this estimator.
- Parameters
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns
- paramsdict
Parameter names mapped to their values.
- set_params(**params)#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters
- **paramsdict
Estimator parameters.
- Returns
- selfestimator instance
Estimator instance.
Examples using nilearn.connectome.ConnectivityMeasure#
Extracting signals of a probabilistic atlas of functional regions
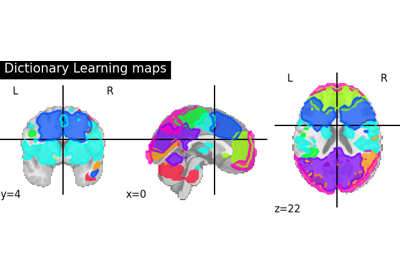
Regions extraction using dictionary learning and functional connectomes
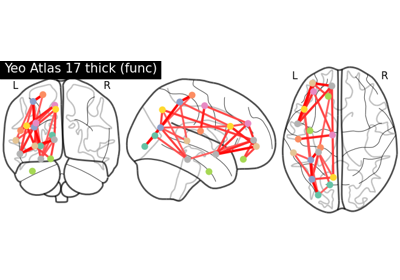
Comparing connectomes on different reference atlases
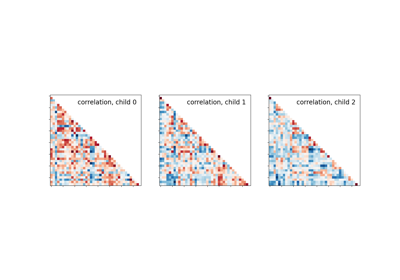
Classification of age groups using functional connectivity