Note
Click here to download the full example code or to run this example in your browser via Binder
Encoding models for visual stimuli from Miyawaki et al. 2008#
- This example partly reproduces the encoding model presented in
Visual image reconstruction from human brain activity using a combination of multiscale local image decoders, Miyawaki, Y., Uchida, H., Yamashita, O., Sato, M. A., Morito, Y., Tanabe, H. C., … & Kamitani, Y. (2008). Neuron, 60(5), 915-929.
Encoding models try to predict neuronal activity using information from presented stimuli, like an image or sound. Where decoding goes from brain data to real-world stimulus, encoding goes the other direction.
We demonstrate how to build such an encoding model in nilearn, predicting fMRI data from visual stimuli, using the dataset from Miyawaki et al., 2008.
Participants were shown images, which consisted of random 10x10 binary (either black or white) pixels, and the corresponding fMRI activity was recorded. We will try to predict the activity in each voxel from the binary pixel-values of the presented images. Then we extract the receptive fields for a set of voxels to see which pixel location a voxel is most sensitive to.
See also Reconstruction of visual stimuli from Miyawaki et al. 2008 for a decoding approach for the same dataset.
Note
If you are using Nilearn with a version older than 0.9.0,
then you should either upgrade your version or import maskers
from the input_data module instead of the maskers module.
That is, you should manually replace in the following example all occurrences of:
from nilearn.maskers import NiftiMasker
with:
from nilearn.input_data import NiftiMasker
Loading the data#
Now we can load the data set:
from nilearn.datasets import fetch_miyawaki2008
dataset = fetch_miyawaki2008()
Dataset created in /home/alexis/nilearn_data/miyawaki2008
Downloading data from https://www.nitrc.org/frs/download.php/8486/miyawaki2008.tgz ...
Downloaded 6504448 of 161069109 bytes (4.0%, 23.8s remaining)
Downloaded 20848640 of 161069109 bytes (12.9%, 13.8s remaining)
Downloaded 33218560 of 161069109 bytes (20.6%, 11.7s remaining)
Downloaded 49258496 of 161069109 bytes (30.6%, 9.2s remaining)
Downloaded 64962560 of 161069109 bytes (40.3%, 7.5s remaining)
Downloaded 80232448 of 161069109 bytes (49.8%, 6.1s remaining)
Downloaded 93134848 of 161069109 bytes (57.8%, 5.2s remaining)
Downloaded 103653376 of 161069109 bytes (64.4%, 4.5s remaining)
Downloaded 114417664 of 161069109 bytes (71.0%, 3.7s remaining)
Downloaded 125820928 of 161069109 bytes (78.1%, 2.8s remaining)
Downloaded 137043968 of 161069109 bytes (85.1%, 1.9s remaining)
Downloaded 148209664 of 161069109 bytes (92.0%, 1.1s remaining)
Downloaded 151060480 of 161069109 bytes (93.8%, 0.9s remaining)
Downloaded 156319744 of 161069109 bytes (97.1%, 0.4s remaining) ...done. (15 seconds, 0 min)
Extracting data from /home/alexis/nilearn_data/miyawaki2008/18b67c55cebe5e71427c5ffdcfafd948/miyawaki2008.tgz..... done.
We only use the training data of this study, where random binary images were shown.
# training data starts after the first 12 files
fmri_random_runs_filenames = dataset.func[12:]
stimuli_random_runs_filenames = dataset.label[12:]
We can use nilearn.maskers.MultiNiftiMasker to load the fMRI
data, clean and mask it.
import numpy as np
from nilearn.maskers import MultiNiftiMasker
masker = MultiNiftiMasker(mask_img=dataset.mask, detrend=True,
standardize=True)
masker.fit()
fmri_data = masker.transform(fmri_random_runs_filenames)
# shape of the binary (i.e. black and wihte values) image in pixels
stimulus_shape = (10, 10)
# We load the visual stimuli from csv files
stimuli = []
for stimulus_run in stimuli_random_runs_filenames:
stimuli.append(np.reshape(np.loadtxt(stimulus_run,
dtype=int, delimiter=','),
(-1,) + stimulus_shape, order='F'))
Let’s take a look at some of these binary images:
import pylab as plt
plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.imshow(stimuli[0][124], interpolation='nearest', cmap='gray')
plt.axis('off')
plt.title('Run {}, Stimulus {}'.format(1, 125))
plt.subplot(1, 2, 2)
plt.imshow(stimuli[2][101], interpolation='nearest', cmap='gray')
plt.axis('off')
plt.title('Run {}, Stimulus {}'.format(3, 102))
plt.subplots_adjust(wspace=0.5)
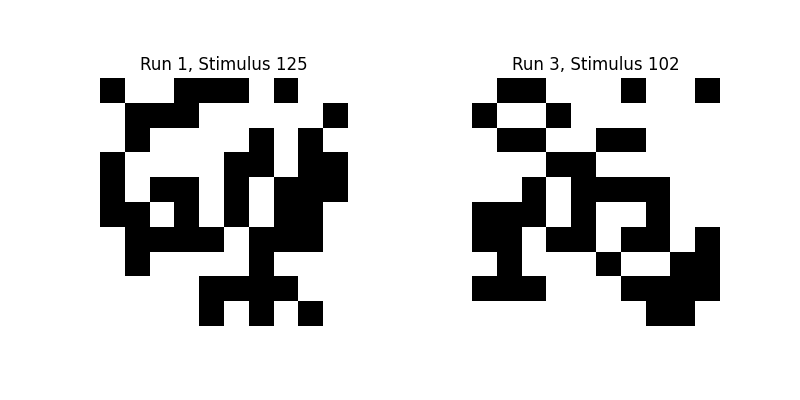
We now stack the fmri and stimulus data and remove an offset in the beginning/end.
fmri_data is a matrix of samples x voxels
print(fmri_data.shape)
(2860, 5438)
We flatten the last two dimensions of stimuli so it is a matrix of samples x pixels.
# Flatten the stimuli
stimuli = np.reshape(stimuli, (-1, stimulus_shape[0] * stimulus_shape[1]))
print(stimuli.shape)
(2860, 100)
Building the encoding models#
We can now proceed to build a simple voxel-wise encoding model using Ridge regression. For each voxel we fit an independent regression model, using the pixel-values of the visual stimuli to predict the neuronal activity in this voxel.
Using 10-fold cross-validation, we partition the data into 10 ‘folds’. We hold out each fold of the data for testing, then fit a ridge regression to the remaining 9/10 of the data, using stimuli as predictors and fmri_data as targets, and create predictions for the held-out 10th.
from sklearn.metrics import r2_score
estimator = Ridge(alpha=100.)
cv = KFold(n_splits=10)
scores = []
for train, test in cv.split(X=stimuli):
# we train the Ridge estimator on the training set
# and predict the fMRI activity for the test set
predictions = Ridge(alpha=100.).fit(
stimuli.reshape(-1, 100)[train], fmri_data[train]).predict(
stimuli.reshape(-1, 100)[test])
# we compute how much variance our encoding model explains in each voxel
scores.append(r2_score(fmri_data[test], predictions,
multioutput='raw_values'))
Mapping the encoding scores on the brain#
To plot the scores onto the brain, we create a Nifti1Image containing the scores and then threshold it:
from nilearn.image import threshold_img
cut_score = np.mean(scores, axis=0)
cut_score[cut_score < 0] = 0
# bring the scores into the shape of the background brain
score_map_img = masker.inverse_transform(cut_score)
thresholded_score_map_img = threshold_img(score_map_img, threshold=1e-6, copy=False)
Plotting the statistical map on a background brain, we mark four voxels which we will inspect more closely later on.
from nilearn.plotting import plot_stat_map
from nilearn.image import coord_transform
def index_to_xy_coord(x, y, z=10):
'''Transforms data index to coordinates of the background + offset'''
coords = coord_transform(x, y, z,
affine=thresholded_score_map_img.affine)
return np.array(coords)[np.newaxis, :] + np.array([0, 1, 0])
xy_indices_of_special_voxels = [(30, 10), (32, 10), (31, 9), (31, 10)]
display = plot_stat_map(thresholded_score_map_img, bg_img=dataset.background,
cut_coords=[-8], display_mode='z', aspect=1.25,
title='Explained variance per voxel')
# creating a marker for each voxel and adding it to the statistical map
for i, (x, y) in enumerate(xy_indices_of_special_voxels):
display.add_markers(index_to_xy_coord(x, y), marker_color='none',
edgecolor=['b', 'r', 'magenta', 'g'][i],
marker_size=140, marker='s',
facecolor='none', lw=4.5)
# re-set figure size after construction so colorbar gets rescaled too
fig = plt.gcf()
fig.set_size_inches(12, 12)
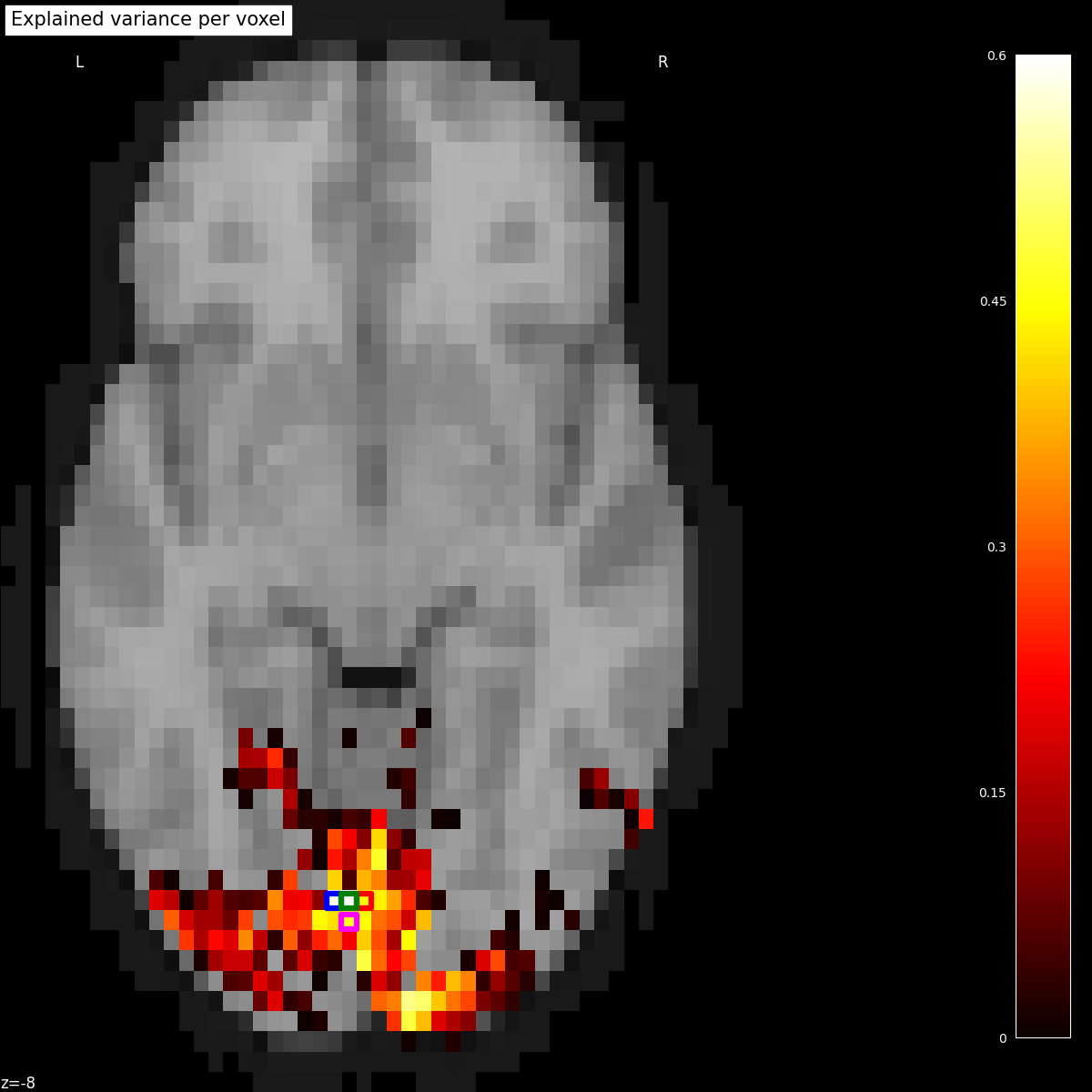
Estimating receptive fields#
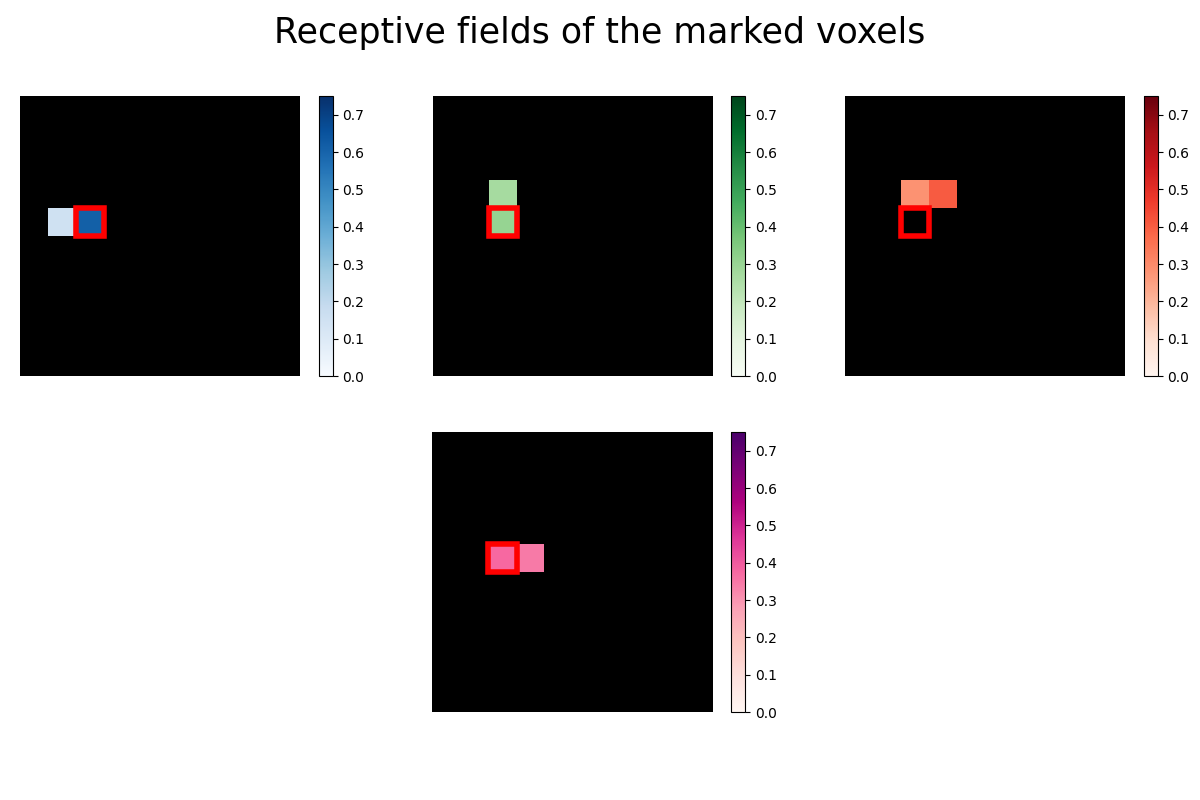
Now we take a closer look at the receptive fields of the four marked voxels. A voxel’s receptive field is the region of a stimulus (like an image) where the presence of an object, like a white instead of a black pixel, results in a change in activity in the voxel. In our case the receptive field is just the vector of 100 regression coefficients (one for each pixel) reshaped into the 10x10 form of the original images. Some voxels are receptive to only very few pixels, so we use Lasso regression to estimate a sparse set of regression coefficients.
from sklearn.linear_model import LassoLarsCV
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
# automatically estimate the sparsity by cross-validation
lasso = make_pipeline(StandardScaler(),
LassoLarsCV(normalize=False, max_iter=10))
# Mark the same pixel in each receptive field
marked_pixel = (4, 2)
from matplotlib import gridspec
from matplotlib.patches import Rectangle
fig = plt.figure(figsize=(12, 8))
fig.suptitle('Receptive fields of the marked voxels', fontsize=25)
# GridSpec allows us to do subplots with more control of the spacing
gs1 = gridspec.GridSpec(2, 3)
# we fit the Lasso for each of the three voxels of the upper row
for i, index in enumerate([1780, 1951, 2131]):
ax = plt.subplot(gs1[0, i])
lasso.fit(stimuli, fmri_data[:, index])
# we reshape the coefficients into the form of the original images
rf = lasso.named_steps['lassolarscv'].coef_.reshape((10, 10))
# add a black background
ax.imshow(np.zeros_like(rf), vmin=0., vmax=1., cmap='gray')
ax_im = ax.imshow(np.ma.masked_less(rf, 0.1), interpolation="nearest",
cmap=['Blues', 'Greens', 'Reds'][i], vmin=0., vmax=0.75)
# add the marked pixel
ax.add_patch(Rectangle(
(marked_pixel[1] - .5, marked_pixel[0] - .5), 1, 1,
facecolor='none', edgecolor='r', lw=4))
plt.axis('off')
plt.colorbar(ax_im, ax=ax)
# and then for the voxel at the bottom
gs1.update(left=0., right=1., wspace=0.1)
ax = plt.subplot(gs1[1, 1])
lasso.fit(stimuli, fmri_data[:, 1935])
# we reshape the coefficients into the form of the original images
rf = lasso.named_steps['lassolarscv'].coef_.reshape((10, 10))
ax.imshow(np.zeros_like(rf), vmin=0., vmax=1., cmap='gray')
ax_im = ax.imshow(np.ma.masked_less(rf, 0.1), interpolation="nearest",
cmap='RdPu', vmin=0., vmax=0.75)
# add the marked pixel
ax.add_patch(Rectangle(
(marked_pixel[1] - .5, marked_pixel[0] - .5), 1, 1,
facecolor='none', edgecolor='r', lw=4))
plt.axis('off')
plt.colorbar(ax_im, ax=ax)
<matplotlib.colorbar.Colorbar object at 0x7ff8f2a20be0>
The receptive fields of the four voxels are not only close to each other, the relative location of the pixel each voxel is most sensitive to roughly maps to the relative location of the voxels to each other. We can see a relationship between some voxel’s receptive field and its location in the brain.
Total running time of the script: ( 0 minutes 40.537 seconds)
Estimated memory usage: 457 MB